Quadrados mágicos - Livro matematica divertida e curiosa (Malba Tahan)

   Tomemos um quadrado e dividamo-lo em 4, 9, 16... quadrados iguais — os quais denominaremos casas.
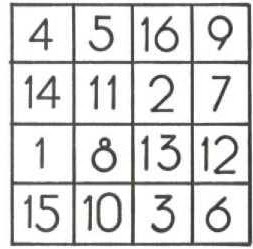
Em cada uma dessas casas, coloquemos um número inteiro. A figura obtida será um quadrado mágico quando a soma dos números que figuram numa coluna, numa linha ou sobre uma diagonal for sempre a mesma. Esse resultado invariável é denominado constante do quadrado, e o número de casas de uma linha é o módulo do quadrado.
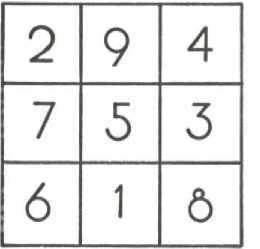
   Os números que ocupam as diferentes casas de um quadrado mágico devem ser todos diferentes. No original desenho de Acquarone figura um quadrado mágico de módulo 3 com a constante igual a 15.
   É obscura a origem dos quadrados mágicos. Acredita-se que a construção dessas figuras constituía já, em época remota, um passatempo que prendia a atenção de um grande número de curiosos.
   Como os antigos atribuíam a certos números propriedades cabalísticas, era muito natural que vissem virtudes mágicas nos arranjos especiais desses números.
   Os quadrados mágicos de módulo ímpar, escreve Rouse
Bali,50 foram construídos na Índia em um período anterior à era
cristã, e introduzidos por Moschopoulos, apareceram na Europa
nos primeiros anos do século XV. Não poucos astrônomos e físicos
da Idade Média estavam convencidos da importância desses arranjos
numéricos. O famoso Cornélio Agrippa (1486-1535) construiu
quadrados mágicos com os módulos 3, 4, 5, 6, 7, 8 e 9, que
representavam, simbolicamente, os sete astros que os astrólogos
daquele tempo denominavam planetas: Saturno, Júpiter, Marte,
Sol, Vênus, Mercúrio e Lua. Para ele o quadrado com uma casa
(módulo 1), tendo nessa casa única o número 1, simbolizava a unidade
e a eternidade de Deus, e como o quadrado com 4 casas não
podia ser construído, ele inferia desse fato a imperfeição dos quatro
elementos: o ar, a terra, a água e o fogo; posteriormente —

acrescenta ainda Rouse Bali — outros escritores afirmaram que esse quadrado devia simbolizar o pecado original. Agrippa, acusado
de exercer feitiçaria, foi condenado a um ano de prisão.
Os orientais, que apreciavam todos os fatos correntes da vida
sob o prisma da superstição, acreditavam que os quadrados
mágicos eram amuletos e serviam de preservativos de certas moléstias.
   Um quadrado mágico de prata, preso ao pescoço, evitava
o contágio da peste.
   Quando um quadrado mágico apresenta certa propriedade,
como, por exemplo, a de ser decomponível em vários quadrados
mágicos, é denominado um quadrado hipermágico.
Entre os quadrados hipermágicos podemos citar os quadrados
diabólicos. São assim denominados os quadrados que continuam mágicos quando transportamos uma coluna ou uma linha de um lado para o outro.
   Entre os quadrados mágicos singulares, poderíamos citar os
bimágicos e os trimágicos.
   Denomina-se bimágico o quadrado que continua mágico
quando elevamos todos os seus elementos ao quadrado. Trimágico é aquele que não perde a sua propriedade quando elevamos os seus elementos ao cubo. Para a construção dos quadrados mágicos, há diversos processos.
   Em 1693, Frenicle de Barry publicou um estudo sobre os quadrados mágicos, apresentando uma lista completa de 880 quadrados mágicos de módulo igual a 9.