Esta é a versão completa de uma charada matemática que ja postei aqui de forma resumida. O texto é um pouco longo mas muito interessante. A versão simples esta nomeada de " O rei e o xadrêz ".
Diz uma antiga lenda que Lahur Sessa ofereceu
ao rei Iodava, senhor de Taligana, o jogo de xadrez
por ele inventado. O monarca, encantado com
o maravilhoso presente, quis dar a Sessa uma recompensa.
E, dirigindo-se ao jovem brâmane, disse-lhe: — Quero recompensar-te, meu amigo, por este maravilhoso
presente que de tanto me serviu para alívio das velhas angústias. Dize-me, pois, o que desejas para que eu possa, mais uma vez, demonstrar o quanto sou grato para com aqueles que se mostram dignos de prémios.
As palavras com que o rei traduzia o generoso oferecimento deixaram Sessa imperturbável. A sua fisionomia serena não traiu a menor emoção, a mais insignificante mostra de alegria ou surpresa. Os vizires olhavam-no atônitos e entreolhavam-se pasmados diante da apatia de uma cobiça a que se dava o direito da
mais livre expansão.
— Rei poderoso! — exclamou o jovem. — Não desejo, pelo presente que hoje vos trouxe, outra recompensa, além da satisfação de ter proporcionado ao senhor de Taligana um passatempo
agradável que lhe vem aligeirar as horas dantes alongadas por uma tristeza acabrunhante. Já estou, portanto, sobejamente aquinhoado e outra qualquer paga seria excessiva.
Sorriu desdenhosamente o bom soberano ao ouvir aquela resposta que refletia um desinteresse tão raro entre os ambiciosos hindus. E, não crendo na sinceridade das palavras de Sessa, insistiu:
— Causa-me assombro a tua simplicidade e o teu desamor
aos bens materiais, ó moço! A modéstia, quando excessiva, é como o vento que apaga o archote, deixando o viandante nas trevas de uma noite interminável. Para que possa o homem vencer os múltiplos obstáculos que se lhe deparam na vida, precisa ter o espírito preso às raízes de uma ambição que o encaminhe a um
ideal qualquer. Exijo, portanto, que escolhas, sem mais demora, uma recompensa digna da tua valiosa oferta. Queres uma bolsa cheia de ouro? Desejas uma arca repleta de jóias? Já pensaste em possuir um palácio? Almejas a administração de uma província? Aguardo a tua resposta por isto que à minha promessa
está ligada a minha palavra!
— Recusar o vosso oferecimento depois de vossas últimas palavras — respondeu Sessa — seria menos uma descortesia do que desobediência ao rei. Vou, pois, aceitar pelo jogo que invente uma recompensa que corresponda à vossa generosidade; não desejo, contudo, nem ouro nem terras ou palácios. Peço o meu pagamento em grãos de trigo.
— Grãos de trigo? — exclamou o rei, sem ocultar o espanto que lhe causava semelhante proposta. — Como poderei pagar-te com tão insignificante moeda?
— Nada mais simples — elucidou Sessa. — Dar-me-eis um grão de trigo pela primeira casa do tabuleiro; dois, pela segunda; quatro, pela terceira, oito, pela quarta; e, assim, dobrando sucessivamente até a sexagésima quarta e última casa do tabuleiro. Peço-vos, ó rei, de acordo com a vossa magnânima oferta, que autorizeis o pagamento em grãos de trigo, e assim como indiquei!
Não só o rei como os vizires e venerandos brâmanes presentes riram-se estrepitosamente ao ouvir a estranha solicitação do tímido inventor. A desambição que ditara aquele pedido era, na verdade, de causar assombro a quem menos apego tivesse aos lucros materiais da vida, O moço brâmane, que bem poderia obter do rei um palácio ou uma província, contentava-se com grãos de trigo!
— Insensato! — exclamou o rei. — Onde foste aprender tão grande desamor à fortuna? A recompensa que me pedes é ridícula. Bem sabes que há, num punhado de trigo, um número incontável de grãos. Deves, compreender, portanto, que com duas ou três medidas de trigo eu te pagarei, folgadamente, consoante o teu pedido, pelas sessenta e quatro casas do tabuleiro. É certo, pois, que pretendes uma recompensa que mal chegará para distrair, durante alguns dias, a fome do último "pária" do meu reino. Enfim, visto que minha palavra foi dada, vou expedir ordens para que o pagamento se faça imediatamente conforme teu desejo.
Mandou o rei chamar os algebristas mais hábeis da corte e ordenou-lhes que calculassem a porção de trigo que Sessa pretendia. Os sábios matemáticos, ao cabo de algumas horas de acurados estudos, voltaram ao salão para submeter ao rei o resultado completo de seus cálculos.
Perguntou-lhes o rei, interrompendo a partida que então jogava:
— Com quantos grãos de trigo poderei, afinal, desobrigarme
da promessa que fiz ao jovem Sessa?
— Rei magnânimo — respondeu o mais sábio dos geômetras.
— Calculamos o número de grãos de trigo que constituirá o pagamento pedido por Sessa, e obtivemos um número49, cuja grandeza é inconcebível pela imaginação humana. Avaliamos, em seguida, com o maior rigor, a quantos sacos corresponderia esse total de grãos, e chegamos à seguinte conclusão: a porção de trigo que deve ser dada a Lahur Sessa equivale a uma montanha que tendo por base a cidade de Taligana, fosse cem vezes mais alta do que o Himalaia! A Índia inteira, semeados todos os seus campos, taladas todas as suas cidades, não produziria, num século, a quantidade de trigo que, pela vossa promessa, cabe, em
pleno direito, ao jovem Sessa!
Como descrever aqui a surpresa e o assombro que essas palavras causaram ao rei ladava e a seus dignos vizires? O sobera no hindu via-se, pela primeira vez, diante da impossibilidade de cumprir a palavra dada.
Lahur Sessa — rezam as crónicas do tempo —, como bom súdito, não quis deixar aflito o seu soberano. Depois de declarar publicamente que abria mão do pedido que fizera, dirigiu-se respeitosamente ao monarca e assim falou:
— Meditai, ó rei, sobre a grande verdade que os brâmanes prudentes tantas vezes repetem: Os homens mais avisados iludemse, não só diante da aparência enganadora dos números, mas também com a falsa modéstia dos ambiciosos. Infeliz daquele que toma sobre os ombros o compromisso de honra por uma dívida cuja grandeza não pode avaliar com a tábua de cálculo de sua própria argúcia. Mais avisado e o que muito pondera e pouco promete! Após ligeira pausa, acrescentou: — Menos aprendemos com a ciência vã dos brâmanes do que com a experiência direta da vida e as suas lições de todo o dia, a toda hora desdenhadas!
O homem que mais vive, mais sujeito está às inquietações morais, mesmo que não as queira. Achar-se-á ora triste ora alegre; hoje fervoroso, amanhã tíbio; já ativo, já preguiçoso; a compostura alternará com a leviandade. Só o verdadeiro sábio, instruído nas regras espirituais, eleva-se acima dessas vicissitudes, paira
por sobre todas essas alternativas. Essas inesperadas e tão sábias palavras calaram fundo no espírito do rei. Esquecido da montanha de trigo que, sem querer, prometera ao jovem brâmane, nomeou-o seu primeiro-vizir. E Lahur Sessa, distraindo o rei com engenhosas partidas de xadrez e orientando-o com sábios e prudentes conselhos, prestou os mais assinalados benefícios ao seu povo e ao país para maior segurança do trono e maior glória de sua pátria.
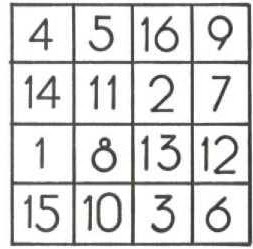 acrescenta ainda Rouse Bali — outros escritores afirmaram que esse quadrado devia simbolizar o pecado original. Agrippa, acusado
acrescenta ainda Rouse Bali — outros escritores afirmaram que esse quadrado devia simbolizar o pecado original. Agrippa, acusado